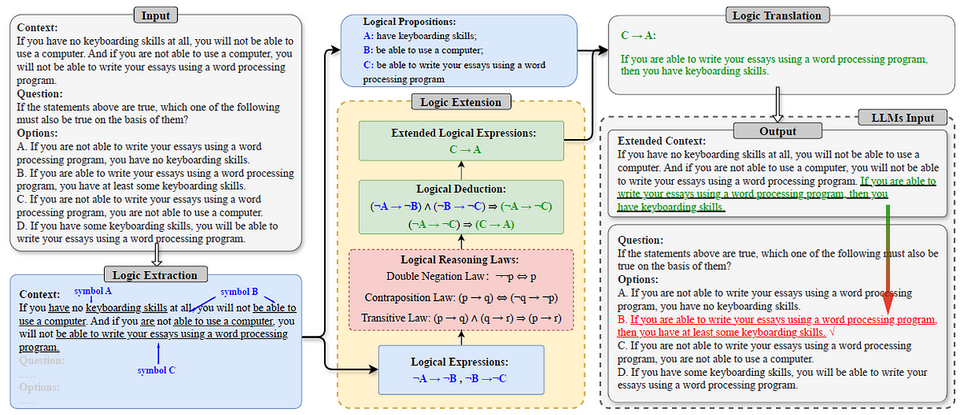
Least-to-Most Prompting: Phương pháp nâng cao khả năng suy luận phức tạp cho mô hình ngôn ngữ lớn

1. Giới thiệu về Least-to-Most Prompting

Least-to-Most Prompting (LtM) là một phương pháp prompt engineering được giới thiệu trong bài báo nghiên cứu "Least-to-Most Prompting Enables Complex Reasoning in Large Language Models" của Zhou và cộng sự, xuất bản trên arXiv vào năm 2022 (Zhou et al., 2022). Phương pháp này được phát triển nhằm khắc phục những hạn chế của các kỹ thuật prompt truyền thống khi đối mặt với các vấn đề phức tạp, đặc biệt là những vấn đề khó hơn so với các ví dụ được cung cấp trong prompt.

Ý tưởng cốt lõi của LtM là chia nhỏ một vấn đề phức tạp thành nhiều bài toán con đơn giản hơn, sau đó giải quyết từng bài toán con theo thứ tự từ đơn giản đến phức tạp, sử dụng kết quả của các bài toán trước làm đầu vào cho các bài toán sau.

2. Cơ chế hoạt động của Least-to-Most Prompting

Phương pháp Least-to-Most Prompting hoạt động qua hai giai đoạn chính:

2.1. Giai đoạn phân rã vấn đề (Decomposition)

Trong giai đoạn này, mô hình ngôn ngữ được hướng dẫn cách chia một vấn đề phức tạp thành các bài toán con đơn giản hơn. Prompt trong giai đoạn này thường chứa các ví dụ minh họa cách phân rã vấn đề, sau đó là câu hỏi cụ thể cần được phân rã.

Ví dụ, nếu cần giải một bài toán phức tạp về tính toán, prompt sẽ hướng dẫn mô hình chia nhỏ bài toán thành các bước tính toán đơn giản hơn.

2.2. Giai đoạn giải quyết các bài toán con (Subproblem Solving)

Sau khi đã phân rã vấn đề, mô hình sẽ lần lượt giải quyết từng bài toán con theo thứ tự. Điểm quan trọng là kết quả của mỗi bài toán con sẽ được sử dụng làm đầu vào cho bài toán tiếp theo, tạo thành một chuỗi giải pháp liên tục.

Quá trình này tiếp tục cho đến khi tất cả các bài toán con đều được giải quyết, và kết quả cuối cùng sẽ là giải pháp cho vấn đề ban đầu.

3. So sánh với Chain-of-Thought Prompting

Least-to-Most Prompting có nhiều điểm tương đồng với Chain-of-Thought (CoT) Prompting, nhưng cũng có những khác biệt quan trọng:

3.1. Điểm tương đồng

• Cả hai phương pháp đều khuyến khích mô hình thực hiện suy luận từng bước.
• Cả hai đều cải thiện khả năng giải quyết vấn đề phức tạp của mô hình ngôn ngữ.
• Cả hai đều có thể được triển khai thông qua few-shot prompting (cung cấp một số ví dụ).

3.2. Điểm khác biệt

• Cấu trúc suy luận: Trong CoT, các bước suy luận thường độc lập và không nhất thiết phải theo thứ tự từ đơn giản đến phức tạp. Trong LtM, các bài toán con được sắp xếp theo thứ tự tăng dần về độ phức tạp.
• Sử dụng kết quả trung gian: LtM sử dụng kết quả của các bài toán con trước làm đầu vào cho các bài toán sau, tạo thành một chuỗi phụ thuộc. CoT không nhất thiết phải có tính phụ thuộc này.
• Khả năng tổng quát hóa: LtM đặc biệt hiệu quả trong việc giải quyết các vấn đề khó hơn so với các ví dụ trong prompt (tổng quát hóa từ dễ đến khó), trong khi CoT thường gặp khó khăn với loại tổng quát hóa này.

4. Hiệu quả của Least-to-Most Prompting

Nghiên cứu của Zhou và cộng sự (2022) đã chứng minh hiệu quả vượt trội của LtM trong nhiều tác vụ phức tạp:

4.1. Xử lý ngôn ngữ SCAN

Trong bài toán SCAN (một benchmark về khả năng tổng quát hóa ngôn ngữ), LtM đạt tỷ lệ thành công 76% với mô hình text-davinci-002, trong khi prompting tiêu chuẩn chỉ đạt 6%. Với mô hình code-davinci-002, LtM đạt tỷ lệ thành công ấn tượng 99.7%.

4.2. Giải quyết bài toán toán học

LtM cũng cho thấy hiệu quả vượt trội trong việc giải quyết các bài toán toán học phức tạp, đặc biệt là những bài toán đòi hỏi nhiều bước tính toán và suy luận.

4.3. Xử lý thao tác ký hiệu

Trong các tác vụ thao tác ký hiệu phức tạp, LtM giúp mô hình ngôn ngữ đạt hiệu suất cao hơn đáng kể so với các phương pháp prompting truyền thống.

5. Triển khai Least-to-Most Prompting

Có hai cách chính để triển khai LtM:

5.1. Triển khai hai giai đoạn

Trong phương pháp này, quá trình được chia thành hai giai đoạn riêng biệt:

1. Giai đoạn phân rã vấn đề: Mô hình được yêu cầu chia vấn đề thành các bài toán con.
2. Giai đoạn giải quyết: Mô hình lần lượt giải quyết từng bài toán con.

5.2. Triển khai một giai đoạn

Trong phương pháp này, cả hai giai đoạn được kết hợp trong một prompt duy nhất. Mô hình được hướng dẫn vừa phân rã vấn đề vừa giải quyết các bài toán con trong cùng một lần tương tác.

6. Ví dụ minh họa

6.1. Ví dụ về bài toán toán học

Vấn đề ban đầu: Tính tổng các số từ 1 đến 100.

Giai đoạn phân rã:

1. Xác định công thức tính tổng dãy số cộng.
2. Xác định số đầu tiên và số cuối cùng trong dãy.
3. Xác định số lượng phần tử trong dãy.
4. Áp dụng công thức để tính tổng.

Giai đoạn giải quyết:

1. Công thức tính tổng dãy số cộng: S = n(a₁ + aₙ)/2
2. Số đầu tiên (a₁) = 1, số cuối cùng (aₙ) = 100
3. Số lượng phần tử (n) = 100
4. Tổng = 100(1 + 100)/2 = 100 × 101/2 = 5050

6.2. Ví dụ về xử lý ngôn ngữ

Vấn đề ban đầu: Dịch câu "jump around twice and then walk" sang ngôn ngữ SCAN.

Giai đoạn phân rã:

1. Phân tích cấu trúc câu thành các thành phần.
2. Dịch từng thành phần sang ngôn ngữ SCAN.
3. Kết hợp các thành phần đã dịch theo đúng cú pháp SCAN.

Giai đoạn giải quyết:

1. Các thành phần: "jump around twice" và "walk"
2. Dịch "jump around": JUMP LEFT, JUMP RIGHT, JUMP FRONT, JUMP BACK
3. Dịch "twice": lặp lại 2 lần
4. Dịch "walk": WALK
5. Kết quả: JUMP LEFT, JUMP RIGHT, JUMP FRONT, JUMP BACK, JUMP LEFT, JUMP RIGHT, JUMP FRONT, JUMP BACK, WALK

7. Ứng dụng thực tế

Least-to-Most Prompting có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau:

7.1. Giáo dục

LtM có thể được sử dụng để tạo ra các hệ thống dạy học thông minh, giúp học sinh giải quyết các bài toán phức tạp bằng cách chia nhỏ thành các bước đơn giản hơn.

7.2. Lập trình

Trong lĩnh vực lập trình, LtM có thể giúp mô hình ngôn ngữ tạo ra mã nguồn phức tạp bằng cách chia nhỏ vấn đề thành các module và chức năng đơn giản hơn.

7.3. Tư vấn và hỗ trợ quyết định

LtM có thể được sử dụng để phân tích các vấn đề kinh doanh hoặc chiến lược phức tạp, giúp các nhà quản lý đưa ra quyết định dựa trên phân tích từng bước.

8. Hạn chế và thách thức

Mặc dù có nhiều ưu điểm, Least-to-Most Prompting vẫn tồn tại một số hạn chế:

8.1. Phụ thuộc vào chất lượng phân rã

Hiệu quả của LtM phụ thuộc rất nhiều vào khả năng phân rã vấn đề thành các bài toán con phù hợp. Nếu việc phân rã không hiệu quả, kết quả cuối cùng có thể không chính xác.

8.2. Tốn kém tài nguyên

LtM thường đòi hỏi nhiều lần tương tác với mô hình hơn so với các phương pháp prompting truyền thống, dẫn đến chi phí tính toán cao hơn.

8.3. Khó khăn trong việc xác định thứ tự tối ưu

Việc xác định thứ tự tối ưu để giải quyết các bài toán con không phải lúc nào cũng đơn giản, đặc biệt là với các vấn đề có nhiều cách tiếp cận khác nhau.

9. Hướng phát triển trong tương lai

Least-to-Most Prompting mở ra nhiều hướng nghiên cứu và phát triển trong tương lai:

9.1. Kết hợp với các kỹ thuật khác

LtM có thể được kết hợp với các kỹ thuật prompt engineering khác như Self-Consistency, Tree-of-Thought, hoặc ReAct để tạo ra các phương pháp mạnh mẽ hơn.

9.2. Tự động hóa quá trình phân rã

Nghiên cứu về việc tự động hóa quá trình phân rã vấn đề có thể giúp giảm sự phụ thuộc vào chất lượng của prompt ban đầu.

9.3. Mở rộng sang các lĩnh vực mới

LtM có tiềm năng được áp dụng trong nhiều lĩnh vực mới như y học, luật pháp, và khoa học dữ liệu, nơi các vấn đề phức tạp thường xuất hiện.

10. Kết luận

Least-to-Most Prompting là một kỹ thuật prompt engineering mạnh mẽ, giúp nâng cao đáng kể khả năng suy luận và giải quyết vấn đề phức tạp của các mô hình ngôn ngữ lớn. Bằng cách chia nhỏ vấn đề thành các bài toán con và giải quyết chúng theo thứ tự từ đơn giản đến phức tạp, LtM giúp mô hình vượt qua những hạn chế của các phương pháp prompting truyền thống.

Với hiệu quả đã được chứng minh trong nhiều tác vụ khác nhau, LtM đang trở thành một công cụ quan trọng trong bộ công cụ của các nhà phát triển AI và người dùng mô hình ngôn ngữ lớn. Khi các mô hình ngôn ngữ tiếp tục phát triển, vai trò của các kỹ thuật như LtM trong việc khai thác tối đa tiềm năng của chúng sẽ ngày càng trở nên quan trọng.

Tài liệu tham khảo

1. Zhou, D., Schärli, N., Hou, L., Wei, J., Scales, N., Wang, X., Schuurmans, D., Bousquet, O., Le, Q., & Chi, E. (2022). Least-to-Most Prompting Enables Complex Reasoning in Large Language Models. arXiv:2205.10625. https://arxiv.org/abs/2205.10625
2. Eliot, L. (2024). Leveraging The Prompt Engineering Technique Known As Least-To-Most Prompting Can Spur Generative AI To Solve Knotty Problems. Forbes. https://forbes.com/sites/lanceeliot/2024/04/02/leveraging-the-prompt-engineering-technique-known-as-least-to-most-prompting-can-spur-generative-ai-to-solve-knotty-problems
3. Novita AI. (2023). How Can Least-to-Most Prompting Enable Complex Reasoning in LLMs? Medium. https://medium.com/@marketing_novita.ai/how-can-least-to-most-prompting-enable-complex-reasoning-in-llms-7580211273d8
4. Learn Prompting. (2024). Least-to-Most Prompting. https://learnprompting.org/docs/intermediate/least_to_most
5. PromptHub Blog. (2024). Least-to-Most Prompting Guide. https://prompthub.us/blog/least-to-most-prompting-guide
6. Greyling, C. (2023). Least To Most Prompting. Medium. https://cobusgreyling.medium.com/least-to-most-prompting-b37ed2e19859